Strain Gauge Load Cell Working Principle
The strain gauge load cell is based on the principle that the elastic element/sensitive beam is elastically deformed under the action of an external force, so that the strain gauge (conversion element) pasted on the surface thereof is also deformed along with the strain gauge. After the strain gauge is deformed, its resistance value will change (increase or decrease), and then the corresponding measurement circuit converts the resistance changes into an electric signal (voltage or current), thereby completing the process of converting external force into electric signals.
As we have mentioned before, the strain gauge load cell is mainly composed of three parts: strain gauge, elastic element and measurement circuit. Now we elaborate on the principles of the strain gauge load cell for these three components.
1. Strain gauge
An important parameter of the strain gauge is the sensitivity coefficient K. Let us introduce the meaning of it.
Suppose there is a metal resistance wire, its length is L and its cross section is a circle of radius r, the area of which is denoted by S, and the resistivity thereof is denoted by ρ, and the Poisson coefficient of this material is μ. When the resistance wire is not subjected to an external force, its resistance value is R:
R = ρL/S(Ω) (1)
When both ends are forced by F, they will elongate, that is, they will be deformed. Suppose its elongation is ΔL, its cross-sectional area is reduced, that is, its cross-sectional radius decreases by Δr. In addition, it can be experimentally proved that the resistivity of the metal resistance wire changes after deformation, which is denoted as Δρ.
Find the full differential for equation (2), that is, how much the resistance value changes after the resistance wire is stretched. We have:
ΔR = ΔρL/S + ΔLρ/S –ΔSρL/S2 (2)
Use equation (1) to devide equation (2)
ΔR/R = Δρ/ρ + ΔL/L – ΔS/S (3)
In addition, we know that the cross-sectional area of the wire is S = πr2, then Δs = 2πr*Δr, so
ΔS/S = 2Δr/r (4)
We know from material mechanics
Δr/r = -μΔL/L (5)
Among them, when the negative sign indicates elongation, the radius direction is reduced. μ is the Poisson coefficient representing the transverse effect of the material. Substituting equation (4)(5) into (3), there is
ΔR/R = Δρ/ρ + ΔL/L + 2μΔL/L
=(1 + 2μ+(Δρ/ρ)/(ΔL/L))*ΔL/L
= K *ΔL/L (6)
Among them
K = 1 + 2μ +(Δρ/ρ)/(ΔL/L) (7)
Equation (6) illustrates the relationship between the rate of change in resistance (relative change in resistance) and the elongation of resistance (relative change in length) of the strain gauge.
It should be noted that the magnitude of the sensitivity coefficient K is a constant determined by the properties of the metal resistance wire material. It is independent of the shape and size of the strain gauge. The K value of different materials is generally between 1.7 and 3.6. Secondly, the K value is a dimensionless quantity.
In material mechanics, ΔL/L is called strain, and it is called ε. It is too large to indicate the elasticity. We often use its one millionth as a unit, record as με. Thus, formula (6) is often written:
ΔR/R = Kε (8)
2. Elastic element
The functions of the elastic element are two. Firstly, it bears the external force of the load cell, and generates a reaction force to the external force to reach a relative static balance.
Secondly, it generates a high-quality strain field/zone, where the strain gauge pasted can ideal complete the conversion task of the strain to electric signal.
Take the elastic element of the beam load cell as an example to introduce the stress distribution.
The center of the bottom of the blind hole is subjected to pure shear stress, but tensile and compressive stresses will appear in the upper and lower parts. The principal stress directions are one for pulling and the other for compressing. If the strain gauge is pasted here, the upper half of the strain gauge will be stretched and the resistance will increase, and the lower half of the strain gauge will be compressed and the resistance will be reduced. The strain expressions at the center of the bottom of the blind hole are listed below and are not derived.
ε = (3Q(1+μ)/2Eb)*(B(H2-h2)+bh2)/ (B(H3-h3)+bh3) (9)
Among them: Q--shear stress for section; E--Young's modulus: μ-Poisson's coefficient; B, b, H, h- are the geometrical dimensions of the beam.
It should be noted that the stress states analyzed above are all "local" cases, and the strain gauges actually feel the 'average' state.
3. Wheatstone bridge
The function of the measuring circuit is to convert the resistance change of the strain gauge into a voltage output. The Wheatstone bridge can suppress the influence of temperature change, can suppress the lateral force interference, and can solve the compensation problem of the load cell more conveniently.
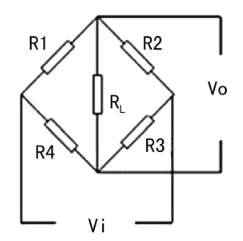
The load cell bridge circuit has RL resistance, and the resistance value is relatively large. For the convenience of analysis, the RL effect is ignored here, which can be understood as the resistance infinity.
VO=VB-VD=R2Vi/(R1+R2)-R3Vi/(R3+R4)=(R2R3+R2R4-R1R3-R2R3)Vi/(R1+R2)(R3+R4) (10)
If we think that Vo = 0, called bridge balance. So the condition of bridge balance is R2R4-R1R3=0, ie R2R4=R1R3. That is, as long as the product of the two pairs of side resistances of the bridge are equal, then the bridge is balanced and its output is equal to zero.
What is said above is the basic characteristics of any Wheatstone bridge. However, most of the load cells use equal arm bridge.
The initial resistance of the four bridge arms are the same, that is, R1=R2=R3=R4, that is, if the resistance does not change, Vo = 0.
Now, let the bridge arm have a small increment plus or minus ΔR under the condition that the original resistance is equal, that is, R1-△R, R2+△R, R3-△R, R4+△R.
VO=[(R+△R)2-(R-△R)2Vi]/4R2=4△RRVi/4R2=△RVi/R (11)
This is the relationship between the full Wheatstone bridge output and the input (excitation voltage). Vo and △R are linear relationships.
When the load cell is not stressed, the bridge is balanced and the signal output is zero. When the load cell receives the force, the strain gauge changes, the bridge resistance changes, the bridge loses balance, and there is a weak voltage signal in output terminal.
As we have mentioned before, the strain gauge load cell is mainly composed of three parts: strain gauge, elastic element and measurement circuit. Now we elaborate on the principles of the strain gauge load cell for these three components.
1. Strain gauge
An important parameter of the strain gauge is the sensitivity coefficient K. Let us introduce the meaning of it.
Suppose there is a metal resistance wire, its length is L and its cross section is a circle of radius r, the area of which is denoted by S, and the resistivity thereof is denoted by ρ, and the Poisson coefficient of this material is μ. When the resistance wire is not subjected to an external force, its resistance value is R:
R = ρL/S(Ω) (1)
When both ends are forced by F, they will elongate, that is, they will be deformed. Suppose its elongation is ΔL, its cross-sectional area is reduced, that is, its cross-sectional radius decreases by Δr. In addition, it can be experimentally proved that the resistivity of the metal resistance wire changes after deformation, which is denoted as Δρ.
Find the full differential for equation (2), that is, how much the resistance value changes after the resistance wire is stretched. We have:
ΔR = ΔρL/S + ΔLρ/S –ΔSρL/S2 (2)
Use equation (1) to devide equation (2)
ΔR/R = Δρ/ρ + ΔL/L – ΔS/S (3)
In addition, we know that the cross-sectional area of the wire is S = πr2, then Δs = 2πr*Δr, so
ΔS/S = 2Δr/r (4)
We know from material mechanics
Δr/r = -μΔL/L (5)
Among them, when the negative sign indicates elongation, the radius direction is reduced. μ is the Poisson coefficient representing the transverse effect of the material. Substituting equation (4)(5) into (3), there is
ΔR/R = Δρ/ρ + ΔL/L + 2μΔL/L
=(1 + 2μ+(Δρ/ρ)/(ΔL/L))*ΔL/L
= K *ΔL/L (6)
Among them
K = 1 + 2μ +(Δρ/ρ)/(ΔL/L) (7)
Equation (6) illustrates the relationship between the rate of change in resistance (relative change in resistance) and the elongation of resistance (relative change in length) of the strain gauge.
It should be noted that the magnitude of the sensitivity coefficient K is a constant determined by the properties of the metal resistance wire material. It is independent of the shape and size of the strain gauge. The K value of different materials is generally between 1.7 and 3.6. Secondly, the K value is a dimensionless quantity.
In material mechanics, ΔL/L is called strain, and it is called ε. It is too large to indicate the elasticity. We often use its one millionth as a unit, record as με. Thus, formula (6) is often written:
ΔR/R = Kε (8)
2. Elastic element
The functions of the elastic element are two. Firstly, it bears the external force of the load cell, and generates a reaction force to the external force to reach a relative static balance.
Secondly, it generates a high-quality strain field/zone, where the strain gauge pasted can ideal complete the conversion task of the strain to electric signal.
Take the elastic element of the beam load cell as an example to introduce the stress distribution.
The center of the bottom of the blind hole is subjected to pure shear stress, but tensile and compressive stresses will appear in the upper and lower parts. The principal stress directions are one for pulling and the other for compressing. If the strain gauge is pasted here, the upper half of the strain gauge will be stretched and the resistance will increase, and the lower half of the strain gauge will be compressed and the resistance will be reduced. The strain expressions at the center of the bottom of the blind hole are listed below and are not derived.
ε = (3Q(1+μ)/2Eb)*(B(H2-h2)+bh2)/ (B(H3-h3)+bh3) (9)
Among them: Q--shear stress for section; E--Young's modulus: μ-Poisson's coefficient; B, b, H, h- are the geometrical dimensions of the beam.
It should be noted that the stress states analyzed above are all "local" cases, and the strain gauges actually feel the 'average' state.
3. Wheatstone bridge
The function of the measuring circuit is to convert the resistance change of the strain gauge into a voltage output. The Wheatstone bridge can suppress the influence of temperature change, can suppress the lateral force interference, and can solve the compensation problem of the load cell more conveniently.

The load cell bridge circuit has RL resistance, and the resistance value is relatively large. For the convenience of analysis, the RL effect is ignored here, which can be understood as the resistance infinity.
VO=VB-VD=R2Vi/(R1+R2)-R3Vi/(R3+R4)=(R2R3+R2R4-R1R3-R2R3)Vi/(R1+R2)(R3+R4) (10)
If we think that Vo = 0, called bridge balance. So the condition of bridge balance is R2R4-R1R3=0, ie R2R4=R1R3. That is, as long as the product of the two pairs of side resistances of the bridge are equal, then the bridge is balanced and its output is equal to zero.
What is said above is the basic characteristics of any Wheatstone bridge. However, most of the load cells use equal arm bridge.
The initial resistance of the four bridge arms are the same, that is, R1=R2=R3=R4, that is, if the resistance does not change, Vo = 0.
Now, let the bridge arm have a small increment plus or minus ΔR under the condition that the original resistance is equal, that is, R1-△R, R2+△R, R3-△R, R4+△R.
VO=[(R+△R)2-(R-△R)2Vi]/4R2=4△RRVi/4R2=△RVi/R (11)
This is the relationship between the full Wheatstone bridge output and the input (excitation voltage). Vo and △R are linear relationships.
When the load cell is not stressed, the bridge is balanced and the signal output is zero. When the load cell receives the force, the strain gauge changes, the bridge resistance changes, the bridge loses balance, and there is a weak voltage signal in output terminal.

