Shear Stress Load Cell Working Principle
Normal stress elastic elements with the cylindric structure, columnar structure and cantilever structure have many defects. For example, huge sensitivity changes caused by loading point changes, poor resistance against eccentric, lateral and torsional load, asymmetry of sensitivity when receiving both stretching and compression load, large height of elastic elements and large height of the gravitational center of assembled electronic scale. In response to these defects, countries throughout the world have developed new-type elastic elements not based on stretching, compression and bending stress but based on shear stress in the early 1970s. These new-type elastic elements are known as the shear stress load cell.
As known to all, shear stress cannot be measured, but it can generate the principal strain with both stretching and compression load, and constituting an angle of 45° with the shear elastic elements' central axis. This is what is required by the load cell made up of Wheatstone bridge. Since the shear stress elastic elements uniformly distributed along the strain stress central axis along the shear strain, changes of the loading points will not influence the output sensitivity. The double-shear resistance strain gauge is pasted on the abdomen plate of the I-shaped cross-section, which is not sensitive to eccentric, lateral and torsional load. At the same time, the sensitivity symmetry is high when receiving stretching load and compression load at the same time. The shear beam-type elastic elements have a small height and the assembled electronic scale has a low gravitational center, which fully overcomes the inherent defects of normal strain elastic elements with the cylindric, columnar and cantilever structure. Every year, shear stress elastic elements with different structures are developed and applied to different electronic weighing instruments, thus ushering a new trend for development of the strain load cell.
Mechanical basis for shear stress elastic elements
The strain area of shear stress elastic elements is a plane stress status receiving pure shear. The principal strain plane (interface with the shear stress as zero) and the maximum main shear stress (interface with the nominal stress as zero) constitute an included angle of 45°. After that the resistance strain gauge pasted at an angle of 45° with the central axis can be confirmed. Two principal strains under both stretching and compression stress and generated by the shear stress can be measured. Through mechanical analysis, it can be found that the principal strain changes along the height of the strain beam in shear stress elastic elements. The stress unit at the center of the neutral axis is at the pure-shear stress state. The normal stress is zero. The main shear stress is the largest and equal to the principal strain constituting an angle of 45° with the central axis. After that, the relationship between the principal stress and the shear stress should be measured. In order to work out the relationship between the principal component, ε , of shear stress elastic elements, and the shear stress, γ, the square unit of the pure shear stress under the plane stress state should be analyzed. The pure shear stress unit and the shear stress direction are shown in below figure:
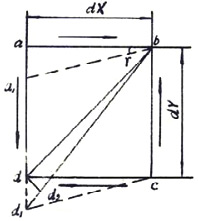
The side length of the square unit is dX=dY. The shear stress exerting on the unit is τ, and the shear strain generated by the shear stress is γ, which turns the unit, abcd, into the unit, a1bcd1, the included angle before and after side deformation of the unit ab and cd is γ, which is the shear strain. The diagonal line, bd, of the unit turns into bd1, with its elongation being d1d2=bd1-bd.
According to the geometric relationship, bd can be written as below:
εbd=(bd1-bd)/bd=d1d2/bd
bd=dX/cos45°
When the deformation is small, ∠dd1d2=45° and d1d2=dd1cos45°. In △dcd1, when shear strain, γ, is small, tanγ=γ and dd1=dX*γ. Therefore,
εbd=d1d2/bd=dd1cos45°/(dX/cos45°)=(dX*γ*1.414/2)/(dX*2/1.414)=γ/2
According to this formula, the length changes of the square unit along the diagonal line is exactly the principal stress orientation under the pure shear strain status. The principal strain, ε, and the shear strain, γ, constitute the following relationship, namely:
ε=γ/2
According to material mechanics, the shear elasticity modulus of isotropic elasticity can be written as below:
G=E/2(1+μ)
The shear strain is:
γ=τ/G=2(1+μ)*τ/E
The principal strain constituting an angle of 45° with the neutral axis of the shear stress elastic elements can be written as below:
ε=±λ/2=±(1+μ)*τ/E
Based on the above analysis, the following conclusions can be reached:
As known to all, shear stress cannot be measured, but it can generate the principal strain with both stretching and compression load, and constituting an angle of 45° with the shear elastic elements' central axis. This is what is required by the load cell made up of Wheatstone bridge. Since the shear stress elastic elements uniformly distributed along the strain stress central axis along the shear strain, changes of the loading points will not influence the output sensitivity. The double-shear resistance strain gauge is pasted on the abdomen plate of the I-shaped cross-section, which is not sensitive to eccentric, lateral and torsional load. At the same time, the sensitivity symmetry is high when receiving stretching load and compression load at the same time. The shear beam-type elastic elements have a small height and the assembled electronic scale has a low gravitational center, which fully overcomes the inherent defects of normal strain elastic elements with the cylindric, columnar and cantilever structure. Every year, shear stress elastic elements with different structures are developed and applied to different electronic weighing instruments, thus ushering a new trend for development of the strain load cell.
Mechanical basis for shear stress elastic elements
The strain area of shear stress elastic elements is a plane stress status receiving pure shear. The principal strain plane (interface with the shear stress as zero) and the maximum main shear stress (interface with the nominal stress as zero) constitute an included angle of 45°. After that the resistance strain gauge pasted at an angle of 45° with the central axis can be confirmed. Two principal strains under both stretching and compression stress and generated by the shear stress can be measured. Through mechanical analysis, it can be found that the principal strain changes along the height of the strain beam in shear stress elastic elements. The stress unit at the center of the neutral axis is at the pure-shear stress state. The normal stress is zero. The main shear stress is the largest and equal to the principal strain constituting an angle of 45° with the central axis. After that, the relationship between the principal stress and the shear stress should be measured. In order to work out the relationship between the principal component, ε , of shear stress elastic elements, and the shear stress, γ, the square unit of the pure shear stress under the plane stress state should be analyzed. The pure shear stress unit and the shear stress direction are shown in below figure:

The side length of the square unit is dX=dY. The shear stress exerting on the unit is τ, and the shear strain generated by the shear stress is γ, which turns the unit, abcd, into the unit, a1bcd1, the included angle before and after side deformation of the unit ab and cd is γ, which is the shear strain. The diagonal line, bd, of the unit turns into bd1, with its elongation being d1d2=bd1-bd.
According to the geometric relationship, bd can be written as below:
εbd=(bd1-bd)/bd=d1d2/bd
bd=dX/cos45°
When the deformation is small, ∠dd1d2=45° and d1d2=dd1cos45°. In △dcd1, when shear strain, γ, is small, tanγ=γ and dd1=dX*γ. Therefore,
εbd=d1d2/bd=dd1cos45°/(dX/cos45°)=(dX*γ*1.414/2)/(dX*2/1.414)=γ/2
According to this formula, the length changes of the square unit along the diagonal line is exactly the principal stress orientation under the pure shear strain status. The principal strain, ε, and the shear strain, γ, constitute the following relationship, namely:
ε=γ/2
According to material mechanics, the shear elasticity modulus of isotropic elasticity can be written as below:
G=E/2(1+μ)
The shear strain is:
γ=τ/G=2(1+μ)*τ/E
The principal strain constituting an angle of 45° with the neutral axis of the shear stress elastic elements can be written as below:
ε=±λ/2=±(1+μ)*τ/E
Based on the above analysis, the following conclusions can be reached:
- Under the plane stress state, the principal strain plane and the maximum shear stress plane constitutes an included angle of 45°. The maximum shear stress and the neutral axis are consistent with each other, so the principal stress constitutes an angle of 45°with the neutral axis. Meanwhile, the pulling stress and the compression stress coexist with an opposite direction but the same value.
-
Under the pure shear stress state, the principal strain receiving both stretching and compression pressure and constituting a 45° angle with the neutral axis is the maximum shear stress. The principal stress should be half of the maximum shear strain. The relationship only exists when the stress unit at the central axis is at the pure shear state, namely:
σ45°=±τmax, ε45°=±γmax/2
- Shear stress cannot be measured, but the principal stress generated by it can be measured via the principal strain. This is what is required by the shear stress elastic elements' pasting bridging form.
-
In the process of design and computing, the formula to work out the maximum shear stress at the neutral axis should be adopted for solution. Below is the Zurawski's shear stress computing formula:
τmax=QS/Jyb
-
The shear force, Q, the interface breadth, b, and the inertia moment, Jy, are constants to an interface, while the static moment, S, is a quantity changing with the position of the shear stress. In other words, the shear stress is a quantity changing with the distance away from the neutral axis. The shear stress distribution rules of the shear beam of different shapes can be worked out, and the equation to work out the shear stress of different cross-sectional shapes is different.

